大学生の日常をちょっとした漫画にしつつ、ちょいちょい大事なことを伝えられればと思います。ちなみに漫画はコミPo!で作成しました。

【漫画】統計の「と」の字を覚えた程度の人が、アレを分析してみた結果…
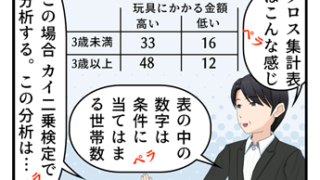
統計学の本をみながら何やら考え込むタイダ君。どうしたのでしょう?




漫画は、感情表現なども簡単なので、文章の限界を超えて伝えられます。漫画を簡単に作成できるコミPo!は強力な表現ツールといえます!
はじめに
統計学を学ぶことは、現代社会で求められる重要なスキルであり、多くのメリットがあります。ここで言いたいには、データを扱わないひとであっても、統計の考え方を学んでおくことは重要って話です。その理由と具体的なメリットを解説します。
データサイエンスとか流行ってるけど統計って何の役にたつの?
データサイエンスって流行ってますね。
そこでは、データを分析するために統計の知識を活用します。統計では、集めたデータをもとに、傾向やパターンを見つけて、的確な判断をします。そのため、統計を学ぶということは、データなどをみたときに、客観的に分析し信頼できる結論を導く力が養われることになります。
では、データを扱わない人にとっては、統計ってあまり役にも立たないものなのでしょうか?
実は、データそのものを扱わなくても、様々な事象に対して個人の主観や思い込みをなくして、正しくものをみていくために統計の考え方が役立ってくるんです。
実際に身につく考え方を以下に示していきますが、他者や物事に対して偏った見方をしたり、騙されて高価な物を購入したりしないようにするためには、けっこう重要と思われます。
あと、まったく無意味な分析結果で誤った結論にも関わらず、その結果を信じてしまって、宝くじの当選番号を予測できると思っちゃう人もいますからね。気を付けたほうがいいですよ。
最後に説明している「詐欺グラフ」なんてものは、有名な経営者とかが使ってたりするそうです。客観的にモノを見る力って本当に重要です。
数値の正しい扱いがわかる
統計を学ぶことで身につく知識の一つに、尺度に関する理解があります。尺度とは、データの種類を分類するための基準で、名義尺度、順序尺度、間隔尺度、比率尺度といった種類があります。この尺度を理解することは、データ分析を行わない人にとっても非常に有益です。
なぜなら、数値がどの尺度に当てはまるかで、使える計算方法が変わってくるからです。
例えば、宝くじの当選番号やビンゴの番号を分析して当ててやるみたいな試みをする人がいますが、そこで出てくる番号の平均値をとったりする操作は誤りです。これらの宝くじの番号は、名義尺度というものに該当し、それぞれの番号に大小や順序の意味はないため、平均を取るなどの計算は適切ではありません。尺度の理解があれば、このような誤解を避けることができます。
以上のように、統計を学ぶことは、データを扱う上での基本的な理解を深め、情報の正確な解釈を可能にするだけでなく、日常生活における情報の質を評価する能力を養うことにも繋がります。4つの尺度や数値の扱いについては、以下に詳しく説明しています。すごく基本ですごく大事な部分です。
データからわかることが何かを理解できる
そもそも統計によって何がわかるか、っていう話ですが、「〇〇のほうが△△よりも多い・大きい」とか、「△△が起こる原因は〇〇だ」とか、分析によってよくそんな結論が出てきたりします。 でも、実際には、直接そんな結論が導かれるわけではありません。
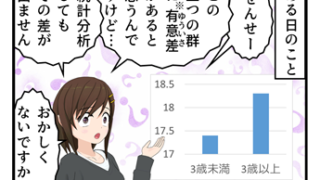
データを分析したときに、「偶然でてきた結果にしては不自然なデータだよね。だから、何らかの傾向とかが働いてそうだね」みたいな結果を出して、「じゃあ、たぶん〇〇と△△の間には、何かしら関係があるんじゃないの」って結論づけるわけです。
データから出てくる結果は、偶然とは思えないような特殊な事象なのかどうかということなんです。その結果に意味をもたせるのは、「仮説」の存在です。
例えば、「学習方法Aをした人の数学の点数は、学習方法Bをした人の数学の点数よりも高い」という仮説があって、学習方法Aの人の点数と学習方法Bの人の点数のデータをとります。その結果、学習方法Aの人の点数が、学習方法Bの人の点数よりも高くて、それが偶然と考えるには不自然なほど違いがあったとなれば、仮説は正しいと判断されることになります。学習方法Aの人の点数が学習方法Bの人の点数より高くても、偶然の範囲でしかない程度だったら、仮説は支持されないことになります。
これがもし、「学習方法Aをした人の数学の点数は、学習方法Bをした人の数学の点数よりも高い」という仮説がなかったり、その仮説を導くための根拠がない状態で分析をしていたとしたら、その結果は何の意味ももちません。
ちなみに、実際の統計では、この仮説に対する帰無仮説を用意するなどのちゃんとした手続きが必要ですが、ここでは置いときます。
あと、一方の数値が高かったとしても「たんなる偶然の範囲」という可能性もあります。 偶然の範囲かどうかは実際に統計的検定が必要になりますが、物事を考えていくときに、何らかの傾向があるとあっさり判断してしまうのではなく、偶然の範囲かどうかに目を向けることも重要です。 「朝、近所のお地蔵さんにあいさつしたら、職場の前で100円を拾った」という経験をしたからといって、「お地蔵さんにあいさつをすると運がよくなる」なんて結論づけちゃダメです。 こんな話は根拠のある仮説をたてようがないし、1回の事象でしかないので、タダの偶然でしかありません。
偏ったものの見方に気付ける
統計を学ぶことの大きなメリットとして、確証バイアスから逃れ、より正確な判断を下す能力を身につけることがあげられます。確証バイアスとは、自分の意見や信念を裏付ける情報を選びがちな傾向のことを指します。このバイアスに囚われると、本来見るべき他の情報を見落とし、偏った判断を下してしまう可能性があります。
例えば、とあるカフェで、アイスコーヒーを注文する人が、同時にケーキも注文しているのを何度か目撃したとします。それをみて、「アイスコーヒーを注文する人はケーキも注文する傾向がある」と結論づけちゃいけません。これを確認するためには、以下のような2×2のクロス集計表で考える必要があります。
| ケーキを注文 | ケーキを注文しない | |
| アイスコーヒーを注文 | a | b |
| アイスコーヒーを注文しない | c | d |
この表には以下のように意味があります。
- a:アイスコーヒーとケーキを両方注文した人の数
- b:アイスコーヒーを注文したがケーキは注文しなかった人の数
- c:アイスコーヒーを注文しなかったがケーキを注文した人の数
- d:アイスコーヒーもケーキも注文しなかった人の数
「アイスコーヒーを注文する人が、同時にケーキも注文しているのを何度か目撃する」というのは、上記の表の a の部分ですが、「アイスコーヒーを注文する人はケーキも注文する傾向がある」と結論づけるためには、b、c、dがどうなっているかを確認しないといけません。a だけじゃなく、c も普通に多いってなったら、アイスコーヒー関係なく、みんなケーキを注文してるって話になります。
「クロス集計表」と同じように扱われる言葉として「分割表」があります。集計したときに度数であれば「分割表」、集計して合計や平均値などを算出した場合を「クロス集計表」という話もあります。が、多くのサイト・書籍で両者を区別しないで説明しています。そして、総務省統計局でも、区別せずにクロス集計表といっているようなので、このサイトでも、とりあえずクロス集計表として統一します。どう扱うのが一番適切なのかはちょっとわかりません。
このようなクロス集計表は、性別や状況などカテゴリーをあらわすデータの分析に適していて、日常のけっこうあらゆる場面で使える考え方です。クロス集計表の考え方は以下にも説明しています。
こういう視点って、確証バイアスによる判断の誤りを避けるためにけっこう重要なわけです。この視点を身につけることで、確証バイアスによる思い込みに目を向けることなく、全体を見渡す客観的な視野を身につけることができます。確証バイアスの代表例の1つとして、血液型と性格の関係の話があるわけですが、それについては以下をご覧ください。
一部の情報から全体がわかったような痛い判断をしなくてすむ
サンプリングと一般化の考え方も大事です。
サンプリングとは、大きなデータ群から一部を選び出すことです。一方、サンプリングによって得られたデータから一般化を行うとは、そのデータを基に全体像を推測することを意味します。
しかし、そもそもサンプリングの時点で偏ったデータを集めていたとしたら、全体像を推測できなくなってしまいます。
実生活においても、自分が確認した一部の情報だけで、全体を傾向がわかったみたいな判断をしないためには、サンプリングと一般化の考え方を知っておくことが大事です。
相関と因果関係の違いがわかる
データ分析を行わない人でも、相関関係と因果関係の違いを理解しておくことって大事です。
例えば、小学校低学年の子どもの身長と学力には相関がある、みたいな話があったとします。相関があるということは、身長が高い子どもは、勉強もよくできているという話です。これを信じて、学力を上げるために身長を伸ばそうとか、身長が高いと黒板の字がよく見えて勉強しやすいかも、なんて誤った方向に話を持っていってはいけません。
実は、小学校低学年だったりもっと低年齢の幼児さんだったりすると、同じ学年であっても、4月生まれなのか、3月生まれなのか(要するに、遅生まれか早生まれか)で約1年程度の発達の違いがあるわけです。そのため、4月生まれの方が身長は高くなりやすいし、物事の理解などがスムーズと思われるので学力も高くなると考えられます。つまり、身長と学力には因果関係があるわけじゃないのに、相関が出てしまうケースです。これを疑似相関と言います。疑似相関については以下に詳しく説明しています。
統計を学ぶことのメリットは、データ分析能力だけでなく、情報を正確に理解し、適切に判断するための思考力を養うことにもあります。統計の知識は、私たちが日常的に直面する情報溢れる世界を理解するための強力な道具となるのです。
詐欺グラフに騙されない
統計を学ぶことの一つのメリットは、詐欺グラフに騙されにくくなるということにもつながります。詐欺グラフとは、データを特定の目的に合わせて誤解を招くように示したグラフのことを指します。これはデータの選択、視覚表現、スケールの設定などにより、データを歪める手法です。
具体的な例を挙げると、ある企業が新製品の売り上げを示すグラフを発表しました。グラフは急激な売り上げ増加を示しています。しかし、詳しく見ると、グラフの縦軸(売り上げ)のスケールが通常とは異なり、本来、無意味な程度の小さな売り上げにも関わらず、グラフでは凄まじい成果があったように見せかけているわけです。
また、グラフの表示期間にも注意が必要です。一部の期間だけを切り出して表示すると、その期間に偶然起こった変動を一般的な傾向として誤解する可能性があります。グラフのデータがどの期間をカバーしているのか、その期間が問題の解釈に適しているのかを考慮することが重要です。
こうした詐欺グラフは、結論ありきでものを語ろうとする人が、手を染めてしまうことがある問題です。グラフに限らないのですが、仮説どおりの結果が出ないと論文にできないと勘違いしている研究者が実際にいて、データを強引に解釈したり、ひどい場合は研究不正に走ったりします。「有意差が出ない」も立派な結果であり、データに真摯に向き合った論文にすることができます。という話が以下の記事にあります。すごく大事な考え方です。
統計では、どんなグラフがどのような意味を持つのか、表示する際の注意点も知ることになります。それによって、詐欺グラフに騙されずに情報を正確に解釈する能力を習得することができます。これは、ビジネスの場面だけでなく、日々の生活においても有用なスキルとなります。
侮るなかれ!統計の考え方を知るために大人にもおすすめできる本
ここで説明したこと以外に「統計がなぜ必要なのか」を知ろうと思ったら、以下の本がおすすめです。
「こども」と書いてあるのですが内容は決して侮れません。この本に書いてある内容を知らない大人はけっこういるからです。小難しい統計の本を読んでわかった気になっているけど、実は、基本的なことをおさえていない人がいます。データサイエンスが流行っているから、データサイエンティストと名乗る人が増えそうだけど、それと同時に、基礎がわかってないナンチャッテデータサイエンティストもけっこういて、これからどんどん増える気がします。例えば以下のような疑問に答えられますか?
- 「統計」っていったい何?
- 統計3大グラフって知ってる?
- 統計ではどんなグラフが使われる? かっこいいだけのグラフは普通は使わないよ(3Dグラフとか、3Dグラフとか、3Dグラフとか・・・)
- 問題解決はどんな手順で考える?
- データはどうやって見つける?
- 統計のよくある間違いを認識してる? 堂々と間違った主張をしかねないよ
「こども統計学」にしっかり書いてある内容です。その意味で、「こども」だけでなく、大学生や社会人でも読む価値があります。こうした疑問に答えられるように、わかりやすい教材でしっかり基礎を身につけましょう!
おわりに
統計学を学ぶことがどのように日常生活やビジネスシーンで役立つのか、具体的な例を交えて解説しました。
統計は、ただデータを解析するための道具というだけではなく、情報を正確に理解し、偏りのない判断を行うための強力な思考法を身につけるためのキーツールとなります。
統計というと難しそうですが、最近では誰もが学びやすいような教材があります。例えば、以下で紹介している本は、ハンバーガーショップという身近な例で店員さんの気持ちになって学べるのでおススメです。
偏った見方をせずに全体を見渡す視野を持つこと、情報が偶然の範囲にあるのか否かを判断すること、そして魅力的に見えるデータ表現に騙されないための視点を身につけることが、統計を学ぶ大きなメリットと言えます。この記事を通じて、統計について少しでも興味を持ってほしいと思います。
卒論のための漫画を作っています!
このブログではちょいちょい自作漫画をお示ししています。
そのほかにも、以下の卒論漫画を作成しており、多数の漫画配信サイトで販売しています。
詳しくは以下で紹介しています。
この漫画は卒論を学ぶことを意図した学習漫画です。
学習漫画は単なる文字+イラストではありません。感情を交えて表現するので、相手に的確に物事を伝える強力な表現方法です。
学習漫画を作ることに興味がある人はぜひ以下の記事をご覧ください。
なお、このブログでは、コミPo!使って漫画を作成しています。頭の中にある妄想を漫画で表現したいと思ったら、手っ取り早く表現することを可能にするツールです。
マニュアルいらずでまずはやってみるで作っていけるのでおすすめです!
無料体験版もありますので、ぜひ活用してみてください!










コメント